Tag Archives for math

The fractional derivative

I have recently had to study some models that use fractional derivatives, which I knew nothing of before. Turns out, these are a lot of fun, and deserve their own post. The notion was apparently already formulated by Leibniz, but there were difficulties involved that kept it from being widely used (such as being, well, bloody difficult). We’re mostly going to ignore those and dive in as if this is a normal thing for a human to do. I want to thank the excellent video at https://www.youtube.com/watch?v=A4sTAKN6yFA for introducing the topic to me this way.

The basis of the idea is simply that the derivative of the integral is the function itself, or

\frac{d}{dx} \int_{-\infty}^x f(t) dt = f(x)

(I’m simplifying here, so just assume that the function has all the nice properties to make this possible). Of course, we will need this to hold for higher orders as well. If we denote by I^n f (x) the function obtained by integrating f n times as follows:

I^n f(x) = \int_{-\infty}^ x \int_{-\infty}^{x_{n}} \cdots \int_{-\infty}^{x_2} f(x_1) dx_1 dx_2 \dots dx_{n}

Fortunately, iterated integrals are not a problem, thanks to the Cauchy integral formula (the other one):

I^n f(x) = \frac{1}{(n-1)!} \int_{-\infty}^x (x-t)^{n-1} f(t) dt.

Remembering that (n-1)! = \Gamma (n), we see there is nothing in the above expression that cannot be generalised to any positive real number (we’ll stick to these for now, lest we get lost too early). Supposing y \in \mathbb{R}^{+}, we define

I^y (x) = \frac{1}{\Gamma (y)} \int_{-\infty}^{x} (x-t)^{y-1} f(t)dt.

There’s a bit of a problem. here regarding integrability. For instance, if you take f(x) = x^2, the above does not work. Instead, we cheat a little by making the lower bound finite:

I^y (x) = \frac{1}{\Gamma (y)} \int_{a}^{x} (x-t)^{y-1} f(t)dt.

We lost uniqueness here, since now we also have to specify the constant a used, but we gain the ability to integrate more functions this way. So, we have a fractional integral, but how do we get to the derivative? By remembering the above relation between derivative and integral, we can set

\frac{d^{y}}{dx^{y}}f(x) = \frac{d^{\lceil y \rceil}}{dx^{\lceil y \rceil}} I^{\lceil y \rceil-y} f(x).

If you look at this informally, you’ll see the derivatives and integrals “cancel out”, except for the integral of order -y, which indicates that this is a derivative of order y.

This particular approach is called the Riemann-Louisville derivative, and it’s not the only one. In fact, there are several definitions of the partial derivative using different kernels – and they’re not equivalent. For the moment though, I think this one illustrates the point well enough, so let’s suspend looking at the others. To see how this would work, let’s compute the 1\frac{1}{2}-th derivative of a simple function, say f(x) = x^2, and see if it makes sense. Since the first derivative is 2x and the second is the constant 2, the 1\frac{1}{2}-derivative should in some sense be “between” these two functions. From the definition, we have to compute

\frac{d^{3/2}}{dx^{3/2}}f(x) = \frac{d^{2}}{dx^{2}} I^{1/2} f(x).

According to our definition, we now need to find

I^{1/2}f(x) = \frac{1}{\Gamma (1/2)} \int_{a}^{x} \frac{t^2}{(x-t)^{1/2}}dt.

\Gamma (1/2) is easy enough to compute (use a substitution to turn it into a Gaussian) and is equal to \sqrt{\pi}. The rest of the integral is not too difficult either – just use the substitution y = (x-t)^{1/2}. This gives us

I^{1/2}f(x) = \frac{16}{15}x^{5/2}.

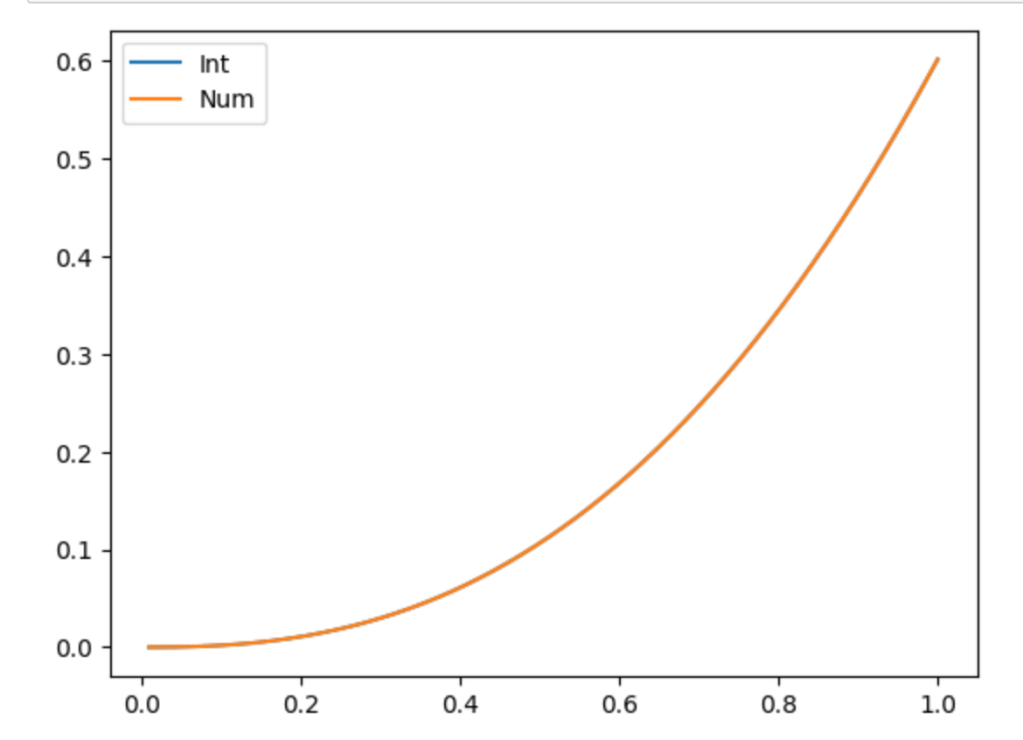
To check our integral, we do it numerically in Python with the script

import numpy as np
import matplotlib.pyplot as plt
import scipy.integrate as integrate

def fun1(t,a,x):
    return (1/np.sqrt(np.pi))*(t**2)/np.sqrt(x-t)

def int0(a,x):
    return integrate.quad(fun1,a,x,args = (a,x))[0]

def check(t):
    return (1/np.sqrt(np.pi))*16*(t**2.5)/15

xspace = np.linspace(1/100,1,1001)# - (5-1)/100,101)

valspace = []
for j in xspace:
    valspace.append(int0(0,j))

valspace0 = check(xspace)

plt.plot(xspace,valspace0, label = 'Int')
plt.plot(xspace,valspace, label = "Num")
plt.legend();

This gives us the following figure, where only one function can be seen, because the two fit snugly on top of each other.

Now that we have some confidence that we’ve evaluated the integral correctly, all we need to do is take the derivative twice to get to the desired 3/2 fractional derivative:

\frac{d^{3/2}}{dx^{3/2}}f(x) = 4x^{1/2}.

Still, does this make sense? There are certainly some intuitive rules that should be followed by our fractional derivative, namely that it should be somehow sandwiched between the integer derivatives, and that there should be a continuity here: we would expect the 0.75th derivative to be closer to the first derivative than the 0.5th one, for instance. Since I don’t want to do an extra bunch of integrals, let’s numerically differentiate some integrals like the above and see if we get closer to the first derivative. But since this post is getting out of hand, let’s leave that for the next one…

Interlude: What’s up with convolution? (Part the first)

You can’t even begin to do Fourier analysis without knowing about the convolution product. But this is a difficult thing to grasp intuitively. I know that I spent many hours trying to understand what’s really going on. There are, as always, really good videos on YouTube about this, which probably explain it better than I ever could, and I urge you to check them out. As for me, when I want to understand something I have to ask why this thing originated, and what it was initially used for. Something like the convolution product does not just drop out of the sky – it had to have some very definite and concrete purpose.

Fortunately, there’s a nice entry at https://math.stackexchange.com/questions/1348361/history-of-convolution that pointed me in the right way – specifically to Laplace, and the theory of probability. Let’s say you have two dice, with sides numbered from 1 to 6 as usual. What is the probability of rolling a seven? To count this we take, say, 1 and asked what should be added to make 7, which is of course 6. We do this for every other number from 2 to 6 (not taking symmetry in to account), and we add the products of the individual probabilities. In other words,

p(1)p(6)+p(2)p(5)+\cdots +p(5)p(2)+p(6)p(1) = \sum_{n=1}^6 p(x)p(7-x).

(In order to have this work for any number between 2 and 12, we would need to assign zero probability to negative numbers.). This at least looks like a convolution, and we can see if a generalization works. See if the same thing works if the second die is now 22-sided, with probabilities given by p_2, and suppose the original dice has probability function p_1. What if the probabilities are not equal (the die is weighted)?

Now we at least have a reasonably intuitive interpretation of convolution in discrete probability. Our goal is to get to the integral however, so let’s see if the same idea works for probability densities. That is, we need to explore whether we get something which computes the probability density or distribution for a sum of random variables \chi_1 and \chi_2. We can try to make this work by analogy (which is how most mathematics is done). Suppose we have functions p_1 and p_2, where

F_i (y) = \mathbb{P}(\{x: \chi_i (x) \leq y \}) = \int_0^y p_i (x) dx, \quad i=1,2/

(We’re assuming the usual Lebesgue measure here, but the same will hold for your other fancy measures – hopefully. I’m assuming the \chi_i are random variables over the reals with reader’s choice of appropriate \sigma-algebra.) We set

p_1 * p_2 (x) = \int p_1 (y) p_2 (x-y) dx

and try to see if there is an analogous interpretation to the discrete case. To get some results we can make sense of without too much effort, we pick two Gaussian distributions, different enough that they are easily distinguished. This would need to be reflected in the convolution product. Let our two probability density functions be given by

p_i (x) = \frac{1}{\sigma_i\sqrt{2\pi} } e^{-\frac{(x-\mu_i)^2}{2\sigma_i^2}}.

Setting \mu_1 = 0, \sigma_1 = 0.2 and \mu_2 = 2, \sigma_2 = 0.25, we get the following graphs for the density functions:

To get the convolution of the density functions p_1 and p_2, we need to evaluate

p_1 * p_2 (x) = \int_{-\infty}^{\infty} p_1 (x-y) p_2 (y) dy,

which gives us the rather nasty-looking

\frac{1}{2\pi \sigma^2 }\int_{-\infty}^{\infty} e^{-\frac{(x-y)^2}{0.08}} e^{-\frac{(y-2)^2}{0.125}} dy.

We could try to calculate this, but instead I’m going to be lazy and just see what it looks like, which is the real point. The Python code below won’t win any prizes, and I’m not using all the library functions I could, but I think it’s pretty clear. The only (perhaps) non-obvious bit is that you have to flip an array before applying the trapezoidal method, because it’s the wrong way round, and you’ll get a negative answer otherwise:

import matplotlib.pyplot as plt
import numpy as np

def normal_dist(x, mu, sd):
    prob_density = np.exp(-0.5*((x-mu)/sd)**2)/(np.sqrt(2*np.pi)*sd)
    return prob_density

xspace = np.linspace(-1,5,601)
yspace = np.linspace(0,3,301)
valspace = []
for t in xspace:
    xyspace = t - yspace
    vals0 = normal_dist(xyspace,0.0,0.2)
    vals1 = normal_dist(yspace,2.0,0.25)
    vals2 = np.multiply(vals0,vals1)
    yspace1 = np.flip(yspace)
    valspace.append(np.trapz(yspace1,vals2))

plt.plot(xspace,valspace)
plt.show

We get the output

Compare this with the two graphs above, and test if the idea of the convolution representing the density of the sum of random variables is still valid. (Not even mentioning that the variables have to be independent, so just be aware of that.)

All of this is excellent, but what does it have to do with Fourier analysis? We’ll get to that next.